В повседневной жизни мы порой попадаемся на маркетинговые уловки: «это выгодно», «открой вклад прямо сейчас», «рассрочка для вас». Часто потому, что не умеем сами посчитать собственную выгоду, а для расчетов достаточно и школьной математики. Предлагаем вам простые формулы, которые позволят понять, что на самом деле происходит с вашими деньгами при разных сценариях.
Эксперт

1. Вы решили оформить вклад. Как посчитать стоимость вашего актива в будущем с учетом инфляции?
— Финансовые организации предлагают нам вклады со ставкой, примерно равной уровню инфляции. Вспомните высокие ставки в 2017-2018 гг., а в прошлом году они были ниже, так как официально инфляция уменьшилась. Для получения прибыли имеет смысл вкладывать деньги, только если ставка по вкладу выше процента инфляции, и от суммы вклада это не зависит. Будущая стоимость актива равна:
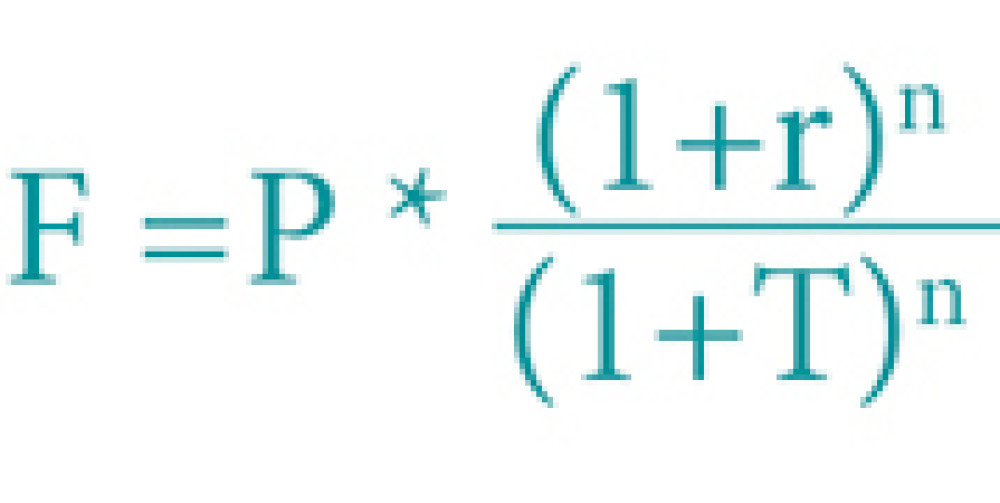
Где F — будущая стоимость актива,
Р — сумма вклада,
Т — темп инфляции по прогнозу ЦБ (сейчас на уровне 3,4 %),
r — процентная ставка в абсолютной величине (проценты/100),
n — срок вклада в годах.
Например, сумма вклада — 100 000 рублей, ставка — 5 % годовых. При инфляции 3,4 % через 1 год получим:
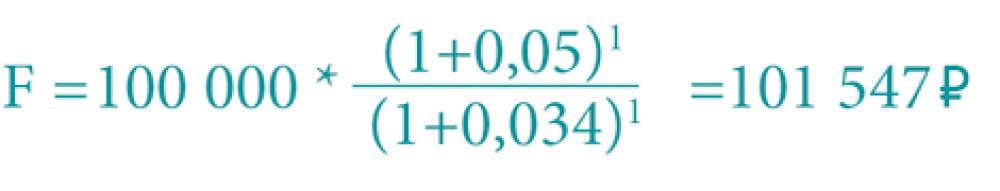
2. Вы никому не доверяете и хранить свои сбережения предпочитаете дома. Как это отразится на покупательной способности ваших денег с учетом инфляции?
— Вклад вряд ли даст большой доход, но вы, по крайней мере, получите деньги с той же платежеспособностью, что и вложили. Возможно, еще чуть-чуть останетесь в плюсе. При этом следует понимать, что и цены вырастут как минимум на величину, пропорциональную уровню инфляции.
Не нужно бояться вкладов, это практически безрисковый финансовый инструмент, к тому же банковские вклады до 1,4 млн рублей застрахованы.
Итак, 100 000 рублей лежат у нас дома «под подушкой». На сколько они подешевеют через год при инфляции в 3,4 %? Считаем:
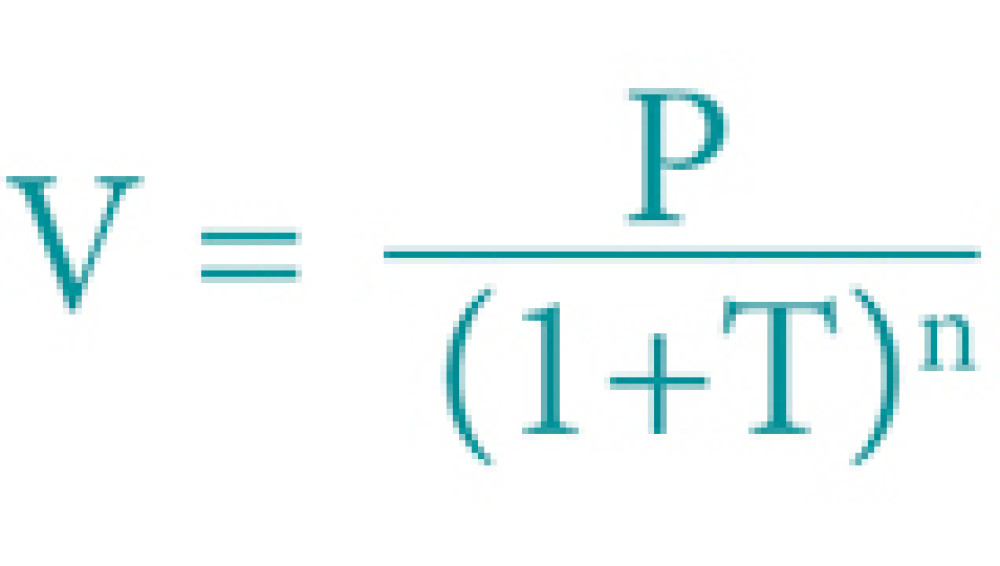
Где V — чистая стоимость в будущем,
Р — сумма сбережений,
Т — темп инфляции по прогнозу ЦБ,
n — срок в годах.
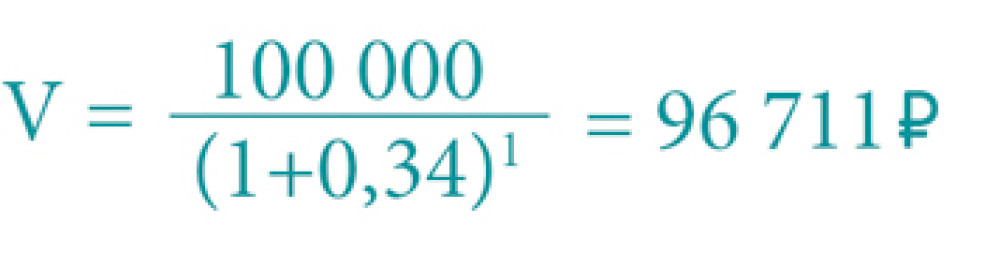
3. Вы все же решили сделать вклад, но условия бывают разные. Как посчитать, в каком случае доход по вкладу будет выше: с выплатой процентов в конце срока или с ежемесячной капитализацией процентов?
— Общее правило: чем чаще капитализация, тем выгоднее клиенту. Даже если ставка вклада с ежемесячной капитализацией ниже, это может оказаться выгоднее в долгосрочном периоде. Поэтому лучше все просчитать заранее и сравнить.
1. Капитализация процентов в конце срока
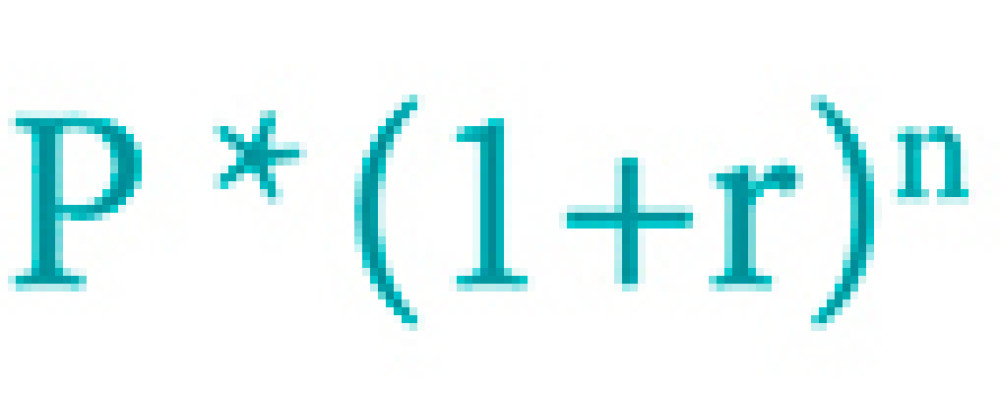
Если наши 100 000 рублей мы положим в банк на 2 года под 5 % годовых, получим:
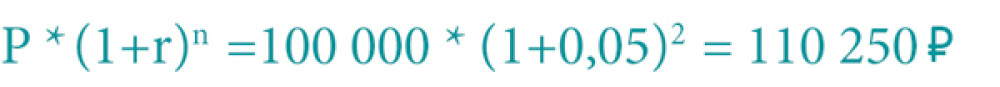
2. Капитализация процентов в конце периода
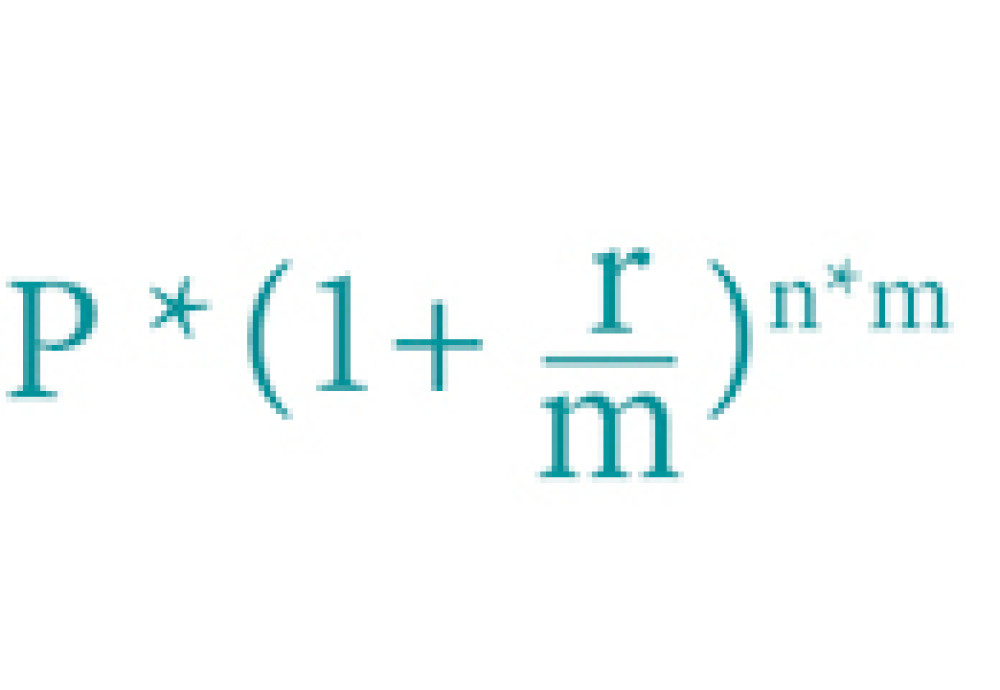
Через 2 года 100 000 рублей на вкладе со ставкой 5 % годовых и с капитализацией в конце каждого месяца дадут:
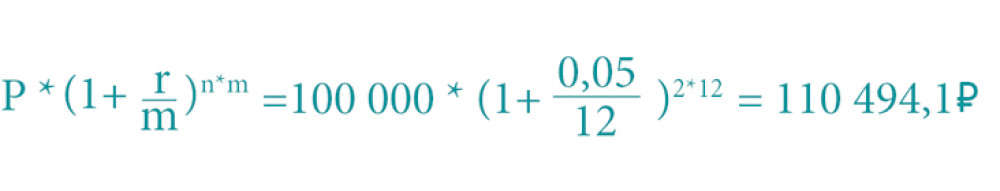
Где Р — сумма вклада,
n — количество лет,
r — процентная ставка в абсолютной величине (проценты/100),
m — количество начислений процентов (капитализаций) в периоде.
4. Иногда банки дают возможность выбрать тип платежа по кредиту — аннуитетный (ежемесячно одинаковый) или дифференцированный (постепенно уменьшающийся). По какой формуле считаются эти платежи и какой из них выгоднее?
— Дифференцированный платеж для клиента выгоднее, но банки не всегда его предлагают. При этом первоначальные платежи будут больше, чем последующие. Не все заемщики могут позволить себе подобный кредит с учетом уровня своего ежемесячного дохода.
Расчет аннуитетного платежа
Для расчета можно использовать формулу:
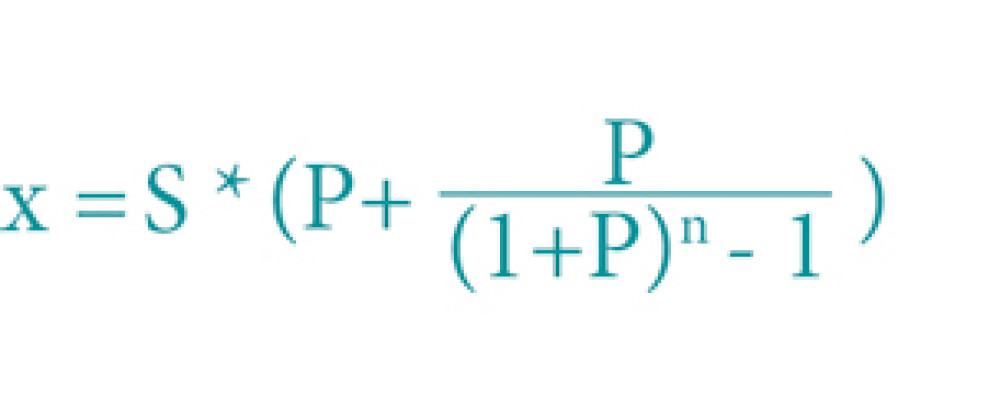
Где x — ежемесячный платеж,
S — первоначальная сумма кредита,
P — 1/12 процентной ставки,
N — количество месяцев.
Формула для определения того, какая часть платежа пошла на погашение кредита, а какая на оплату процентов, является достаточно сложной. Поэтому мы рассчитаем эти суммы простым способом, дающим такой же результат.
Для расчета процентной составляющей аннуитетного платежа нужно остаток кредита на указанный период умножить на годовую процентную ставку и результат поделить на 12 (количество месяцев в году): Pn = Sn * P/12
Где Pn — начисленные проценты,
Sn — остаток задолженности на период,
P — годовая процентная ставка по кредиту.
Чтобы определить часть, идущую на погашение долга, необходимо из ежемесячного платежа отнять начисленные проценты:
S = X-Pn
Где S — часть платежа, идущая на погашение долга,
X — ежемесячный платеж,
Pn — начисленные проценты на момент n-й выплаты.
Так как часть, идущая на погашение основного долга, зависит от предыдущих платежей, вычислять нужно последовательно, начиная с первого платежа.
Пример расчета графика выплат по кредиту с аннуитетными платежами
Например, сумма кредита — 100 000 рублей, годовая ставка — 10 %, срок — 6 месяцев. Для начала рассчитаем ежемесячный платеж:
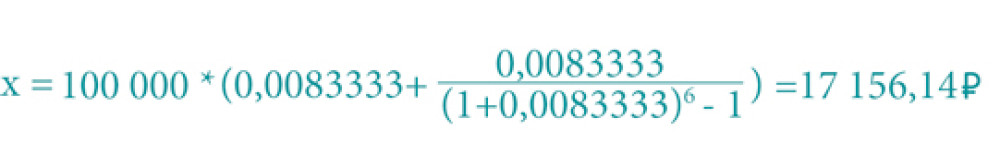
Теперь рассчитаем по месяцам процентную и кредитную части платежа
1-й месяц
Проценты: 100 000 * 0,1 / 12 = 833,33 ₽
Основной долг: 17 156,14 - 833, 33 = 16 322,81 ₽
2-й месяц
Остаток кредита: 100 000 - 16 322,81 = 83 677,19 ₽
Проценты: 83 677,19 * 0,1/12 = 697,31 ₽
Основной долг: 17 156,14 - 697,31 = 16 458,83 ₽
…
6-й месяц
Остаток кредита: 33 888,09 - 16 873.74 = 17 014,35 ₽
Проценты: 17 014,35 * 0,1/12 = 141,79 ₽
Основной долг: 17 156,14 - 141,79 = 17 014,35 ₽
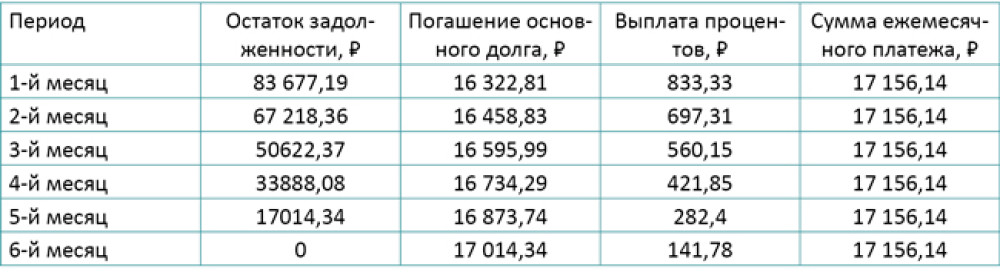
Чтобы узнать размер переплаты по кредиту с аннуитетными платежами, необходимо ежемесячный платеж умножить на количество периодов и из полученного числа вычесть первоначальный размер кредита. В нашем примере переплата составит 2 936,84 ₽.
Расчет дифференцированного платежа
Дифференцированный ежемесячный платеж по кредиту состоит из двух частей — основного платежа и процентов. Основной платеж не меняется в течение всего срока кредитования и идет на погашение основного долга. Сумма, идущая на уплату процентов, уменьшается к концу срока кредитования.
Размер основного платежа вычисляется следующим образом: сумму кредита делим на количество месяцев, за которое планируем погасить кредит, полученное число и будет являться основным платежом.
b = S / N
Где b — основной платеж,
S — размер кредита,
N — количество месяцев.
Для расчета начисленных процентов нужно остаток кредита на указанный период умножить на годовую процентную ставку и результат разделить на 12 (количество месяцев в году).
p = Sn * P/12
Где p — начисленные проценты,
Sn — остаток задолженности на период,
P — годовая процентная ставка по кредиту.
Чтобы рассчитать остаток задолженности на период (Sn), необходимо размер основного платежа умножить на количество прошедших периодов и результат вычесть из общей суммы платежа.
Sn = S - (b*n)
Где n — количество прошедших периодов.
Пример расчета графика выплат по кредиту с дифференцированными платежами
Условия те же: сумма кредита — 100 000 рублей, годовая ставка — 10 %, срок — 6 месяцев. Основной платеж составит: 100 000/6 = 16 666,67 руб.
Определим размер выплаты за каждый месяц периода кредитования:
1-й месяц: 16 666,67 + (100 000 - (16 666,67 * 0))*0,1/12 = 17 500 ₽
2-й месяц: 16 666,67 + (100 000 - (16 666,67 * 1))*0,1/12 = 17 361,11 ₽
…
6-й месяц: 16 666,67 + (100 000 - (16 666,67 * 5))*0,1/12 = 16 805,56 ₽
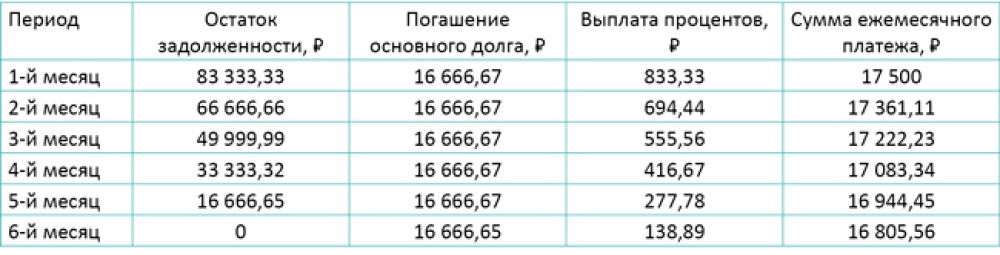
Для расчета суммы переплаты по кредиту необходимо сложить ежемесячные выплаты и вычесть из их суммы первоначальный размер кредита. Для нашего примера переплата составит 2 916,67 ₽.
Для упрощения расчетов рекомендуем воспользоваться сервисами на сайте финкалькулятор.рф, созданном в рамках проекта «Ваши личные финансы». Сервис позволяет сделать расчеты по вашим данным и выгрузить результаты в удобный для вас формат.
Фото: Артём Изофатов